고정소수점, 부동소수점 관한 이야기

프로그래밍 하다보면 실수 계산이 정확하지 않다는 말이 있습니다.
대학시절에 교수님이 말할때도 흘려보냈고 밥벌이로 코딩하면서도 크게 신경쓰지 않았습니다.

요즘 쓰는 한성 노트북 때문에 NTP 관련을 찾아보다가 NTP 프로토콜에 시간값이 Fixed Point로 처리하는걸 보고 좀 더 검색해보다가 알게 된것을 여기에 정리해둡니다.

 

1. 고정소수점(Fixed Point)
고정소수점(Fixed Point)방식은 소수점 이상/이하를 특정 비트로 딱 나눠서 처리합니다.
4바이트 float을 정수부(16비트) 실수부(16비트) 씩 나누거나 아님 정수부(8비트) 실수부(24비트) 이런식으로 나눌수 있는것입니다.
연산을 할때 정수부분보다 실수부분을 정밀하게 처리하도록 하고 싶다면 실수부분에 더 많은 비트를 할당할 수 있는것이지요.

그럼 12.34를 2바이트에 저장하고 정수부와 실수부는 각각 1바이트씩 표현한다고 했을때
12는 2진수 8비트로 표현하면
12/2 = 6 0
6/2  = 3 0
3/2  = 1 1
1/2  = 0 1
0000 1100 이렇게 8비트가 되고 (마지막부터 위로 올라가면서 비트 체크)

.34는 2진수 8비트로 표현면
0.34*2 = 0.68 0
0.68*2 = 1.36 1
0.36*2 = 0.72 0
0.72*2 = 1.44 1
0.44*2 = 0.88 0
0.88*2 = 1.76 1
0.76*2 = 1.52 1
0.52*2 = 1.04 1
0101 0111 이렇게 8비트가 됩니다. (순서대로 비트 체크)

이걸 합쳐서 0000 1100 0101 0111 하면 12.34의 2바이트(1:1) Fixed Point 표현방법이 되죠.
(앞에 부호비트는 걍 생략했습니다.) 참고로 부호비트는 0이면 양수 1이면 음수입니다.

 

2. 부동소수점(Float Point)
이번엔 대부분의 컴퓨터 언어에서 실수형 자료형으로 쓰이는 방식입니다.
이 방식은 IEEE에서 지정한 IEEE754 방식입니다.
IEEE 754는 아래 그림과 같은 방식으로 표현됩니다.

(이미지 출처: 위키피디아 https://ko.wikipedia.org/wiki/IEEE_754 )

부호비트는 sign
지수부는 exponent
가수부는 fraction 으로 표기합니다.

고정소수점에서 썻던 12.34를 부동소수점 방식으로 표현해 봅시다.
– 양수이므로 부호부는 0입니다.
– 절대값을 2진법으로 표현합니다.
정수부분은 1100 으로 짧게 끝납니다. (위에 사용한 예시에 의해)
소수점이하부분은 23비트니 23번 해줍니다.

0.34*2 = 0.68 0
0.68*2 = 1.36 1
0.36*2 = 0.72 0
0.72*2 = 1.44 1

0.44*2 = 0.88 0
0.88*2 = 1.76 1
0.76*2 = 1.52 1
0.52*2 = 1.04 1

0.04*2 = 0.08 0
0.08*2 = 0.16 0
0.16*2 = 0.32 0
0.32*2 = 0.64 0

0.64*2 = 1.28 1
0.28*2 = 0.56 0
0.56*2 = 1.12 1
0.12*2 = 0.24 0

0.24*2 = 0.48 0
0.48*2 = 0.96 0
0.96*2 = 1.92 1
0.92*2 = 1.84 1

0.84*2 = 1.68 1
0.68*2 = 1.36 1
0.36*2 = 0.72 0

1100.01010111000010100011110
이렇게 나옵니다.

이제 소수점을 왼쪽으로 이동시킵니다.
1.10001010111000010100011110*2^3
이렇게 소수점 옮기는거 때문에 부동소수점이라고 불린답니다.
(부동에 부가 浮 뜰부 입니다. 두둥실 떠다닌다고 부동이라고 한답니다.)

그럼 가수부는 구했습니다.
맨앞에 1을 제외한 1000 1010 1110 0001 0100 011이지요. (23비트니 나머진 버립니다)

이젠 지수부를 구할 차례입니다.
지수부는 8비트라 0~255까지 값을 가집니다. 음수양수 지원하면 -128~127의 범위죠.
그래서 0값이 부호없는 수로 하면 127이라 127을 Bias라고 표현합니다.
실제 지수부는 아까 1.10001010111000010100011110*2^3 에서
승수인 3에다가 Bias인 127을 더한값(130)의 이진수인 1000 0010이 들어갑니다.

그래서 결론적으로 12.34를 float형식(IEEE 754) 형식으로 저장하면

0 1000 0010 1000 1010 1110 0001 0100 011
이렇게 됩니다.

 

3. 결론
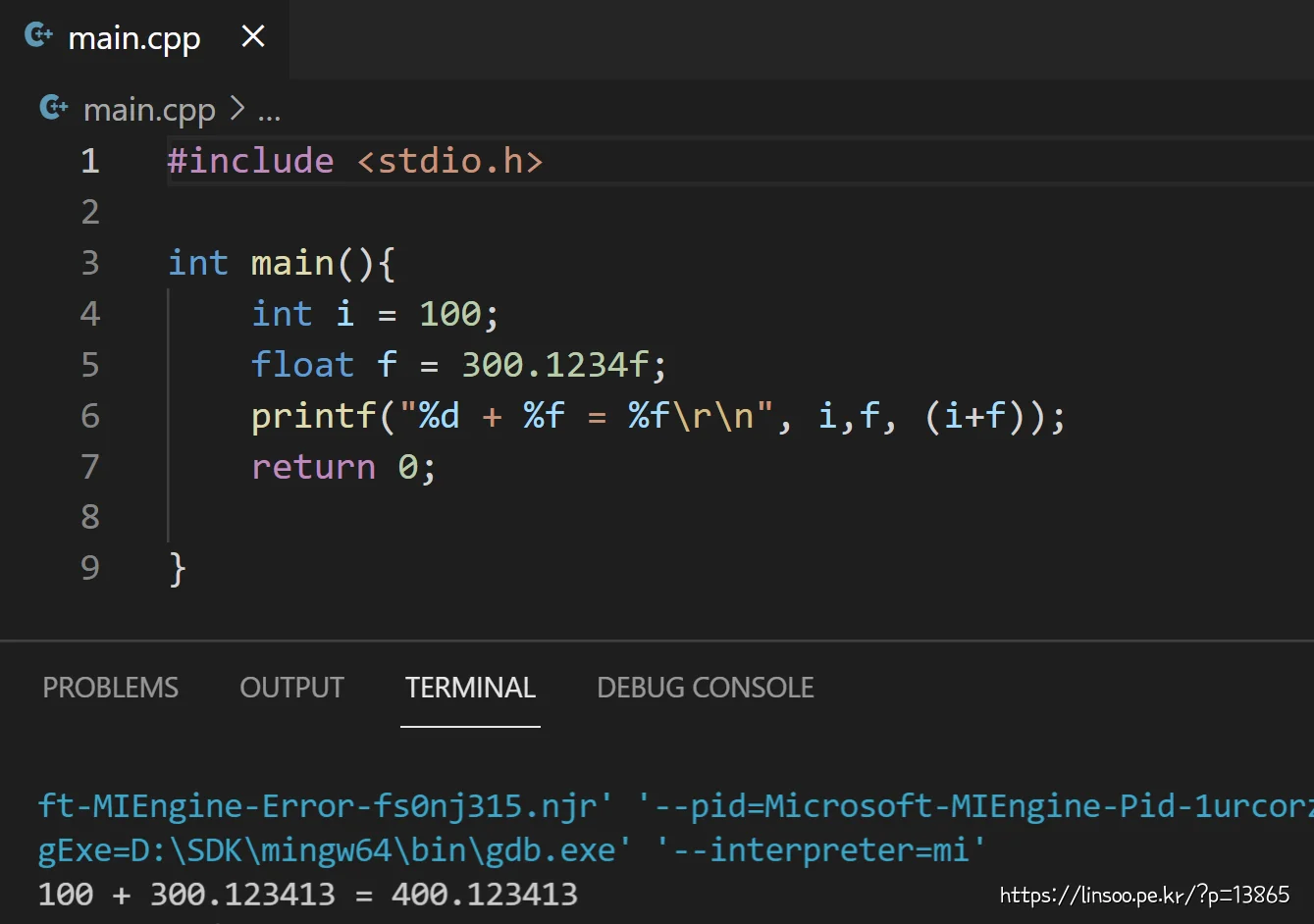
이 글 시작할때 “소수점 처리 방식에 의해 실수 계산이 정확하지 않다는 말” 라는 떡밥을 뿌리고 시작했습니다. 첫 짤에서도 300.1234를 넣었는데 printf하면 300.123413이 나오죠
그 정확하지 않는 이유는 본문에 나옵니다.

고정소수점이던 부동소수점이던 소수점 아래 부분계산할때 2를 곱해서 1이상 큰부분이 비트가 되고 나머진 다시 2를 곱해서 다음자리 비트를 구하는 부분이 있습니다.
이게 딱 1.0 되서 끝나지 않는 이상 계속 쭈욱 가게 되죠.
그래서 값 넣을땐 300.1234를 넣었지만 꺼낼땐 300.123413 이렇게 나오는겁니다.

위 예제는 약간 극단적이라 할수 있긴 한데요.
예전에 다른 사이트에서 본걸론 정확한 값은 기억 나지 않지만 대충 예를 들면 300.0을 넣었는데 꺼낼땐 300.0000000000007 이런식으로 꺼내질수 있다는겁니다.
나누기를 딱 23개만 하는게 아니라 소수점 이동에 따라 23비트 혹은 더 적게 아님 많게 뺑뺑이를 도니깐요.

뭐 아무튼 왜 이런 방식을 했냐고는 IEEE에 따지시고.

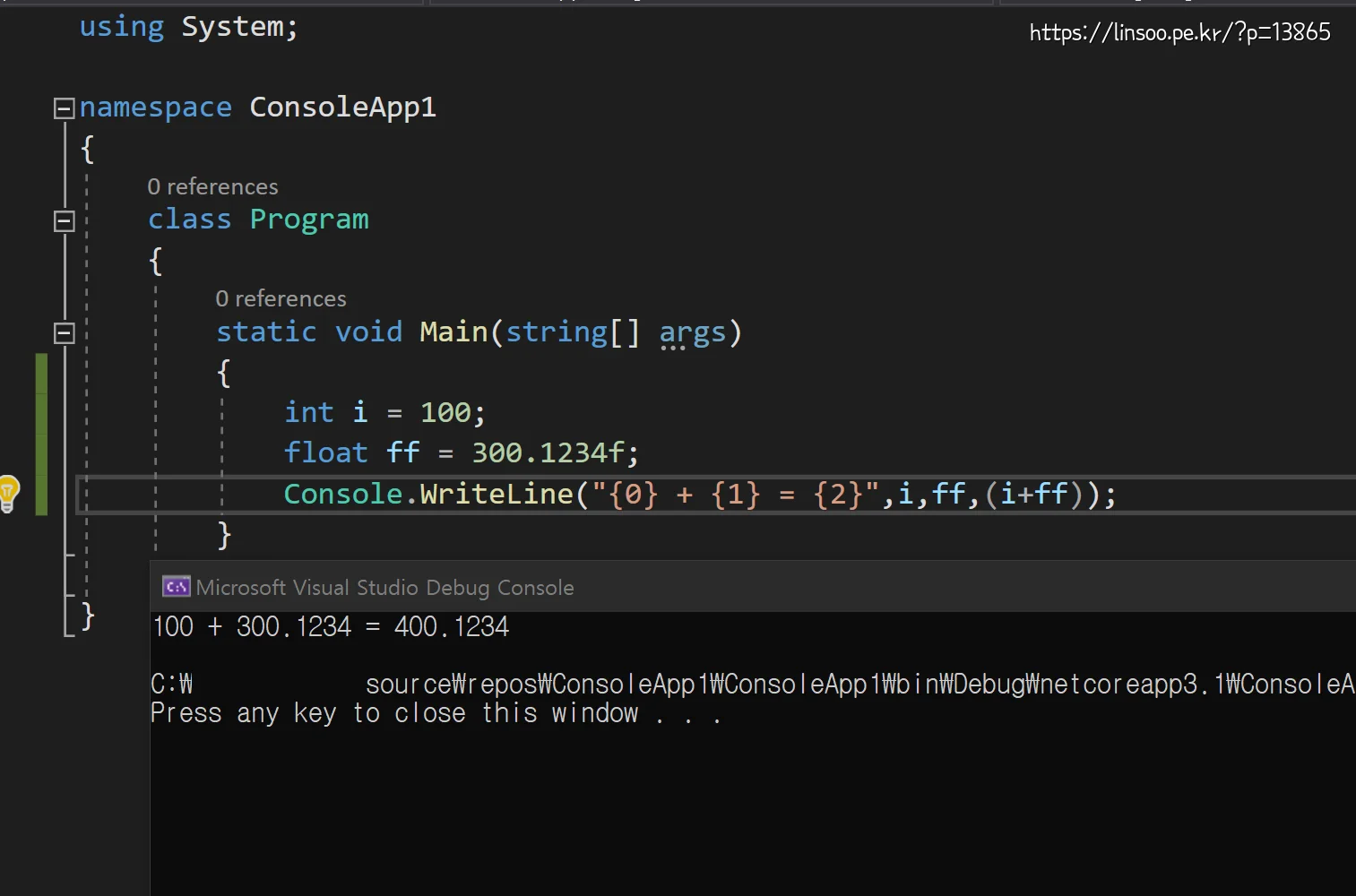
근데 C#에선 잘 나오네요. ㅋㅋㅋㅋ C#은 뭔가 보강을 한건가 아님 WriteLine에서 보정하는건가

참고사이트 :
https://ko.wikipedia.org/wiki/IEEE_754
http://www.matlabinuse.com/Mastering_MATLAB/10359